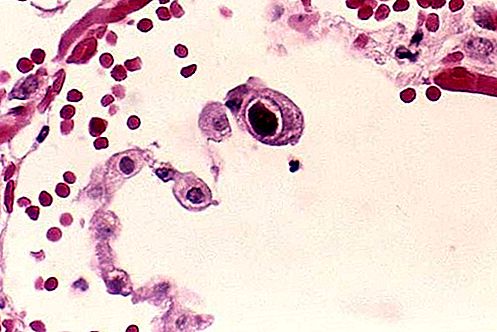
أظهر أبقراط خيوس (fl. c. 460 قبل الميلاد) أن المناطق على شكل القمر بين الأقواس الدائرية ، والمعروفة باسم lunes ، يمكن التعبير عنها تمامًا كمنطقة مستقيمة أو تربيعية. في الحالة البسيطة التالية ، يوجد لونان تم تطويرهما حول جانبي المثلث الأيمن بمساحة مجمعة مساوية لتلك المثلث.
-
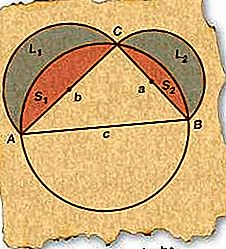
بدءًا من ΔABC الأيمن ، ارسم دائرة يتطابق قطرها مع AB (الجانب c) ، الوتر. لأن أي مثلث قائم على قطر دائرة لوترها يجب أن يكون منقوشًا داخل الدائرة ، يجب أن يكون C على الدائرة.
-
ارسم نصف دائري بأقطار AC (جانب ب) و BC (جانب أ) كما في الشكل.
-
قم بتسمية Lunes الناتج L 1 و L 2 والأجزاء الناتجة S 1 و S 2 ، كما هو موضح في الشكل.
-
الآن يجب أن يساوي مجموع Lunes (L 1 و L 2) مجموع الدوائر (L 1 + S 1 و L 2 + S 2) التي تحتوي عليها ناقص القطعتين (S 1 و S 2). وبالتالي ، L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (حيث أن مساحة الدائرة π ضرب مربع نصف القطر).
-
مجموع المقاطع (S 1 و S 2) يساوي مساحة نصف الدائرة بناءً على AB ناقص مساحة المثلث. وبالتالي ، S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
استبدال التعبير في الخطوة 5 في الخطوة 4 ومعالجة المصطلحات الشائعة ، L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
منذ ∠ACB = 90 درجة ، أ 2 + ب 2 - ج 2 = 0 ، بواسطة نظرية فيثاغورس. وبالتالي ، L 1 + L 2 = ΔABC.
تمكن أبقراط من تربيع عدة أنواع من الرئة ، بعضها على أقواس أكبر وأقل من نصف دائرة ، وقد ألمح ، على الرغم من أنه ربما لم يعتقد ، أن طريقته يمكن أن تربيع دائرة كاملة. في نهاية العصر الكلاسيكي ، ذكر Boethius (حوالي 470-524) ، الذي ستبقي ترجماته اللاتينية لمقتطفات Euclid ضوء وميض الهندسة لمدة نصف الألفية ، أن شخصًا قد أنجز تربيع الدائرة. ما إذا كان العبقري غير المعروف يستخدم lunes أو طريقة أخرى غير معروفة ، لأنه لعدم وجود مساحة Boethius لم تقدم المظاهرة. وهكذا نقل تحدي تربيع الدائرة مع أجزاء من الهندسة مفيدة على ما يبدو في أدائها. ظل الأوروبيون في مهمة سيئة الحظ في عصر التنوير. أخيرًا ، في عام 1775 ، رفضت أكاديمية باريس للعلوم ، التي سئمت من مهمة اكتشاف المغالطات في العديد من الحلول المقدمة لها ، أن يكون لها أي علاقة أخرى بالمربعات الدائرية.