مقطع مخروطي ، يسمى أيضًا مخروطي ، في الهندسة ، أي منحنى ناتج عن تقاطع مستوى مخروط دائري. اعتمادًا على زاوية المستوى بالنسبة للمخروط ، فإن التقاطع هو دائرة ، أو قطع ناقص ، أو زائدة ، أو قطع مكافئ. تحدث حالات التقاطع الخاصة (المنحلة) عندما يمر المستوى عبر القمة فقط (ينتج نقطة واحدة) أو من خلال القمة ونقطة أخرى على المخروط (ينتج خطًا مستقيمًا واحدًا أو خطين مستقيمين متقاطعين). انظر الشكل.
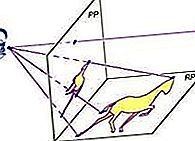
الهندسة الإسقاطية: أقسام مخروطية إسقاطية
يمكن اعتبار المقطع المخروطي أجزاء مستوية من مخروط دائري (انظر الشكل). من خلال
يمكن تتبع الأوصاف الأساسية ، ولكن ليس الأسماء ، للأجزاء المخروطية إلى Menaechmus (ازدهرت حوالي 350 قبل الميلاد) ، تلميذ لكل من أفلاطون و Eudoxus من Cnidus. أعطى Apollonius of Perga (حوالي 262-190 قبل الميلاد) ، والمعروف باسم "المقياس العظيم" ، الأجزاء المخروطية أسماءها وكان أول من حدد فرعي الغلو (الذي يفترض المخروط المزدوج). تعد أطروحة أبولونيوس المكونة من ثمانية مجلدات في الأقسام المخروطية ، Conics ، واحدة من أعظم الأعمال العلمية من العالم القديم.
تعريف تحليلي
يمكن وصف المخروطات أيضًا بأنها منحنيات مستوية هي مسارات (مكان) نقطة تتحرك بحيث تكون نسبة المسافة من نقطة ثابتة (التركيز) إلى المسافة من خط ثابت (Directrix) ثابتًا ، يسمى انحراف المنحنى. إذا كان الانحراف صفرًا ، يكون المنحنى دائرة ؛ إذا كان يساوي واحد ، القطع المكافئ ؛ إذا كان أقل من واحد ، القطع الناقص ؛ وإذا كان أكبر من واحد ، فقرة مفرطة. انظر الشكل.
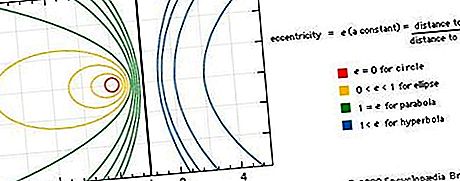
يتوافق كل مقطع مخروطي مع الرسم البياني لمعادلة متعددة الحدود من الدرجة الثانية للصيغة Ax 2 + By 2 + 2Cxy + 2Dx + 2Ey + F = 0 ، حيث x و y متغيرات و A ، B ، C ، D ، E ، و F هي معاملات تعتمد على مخروط معين. من خلال اختيار مناسب لمحاور الإحداثيات ، يمكن اختزال معادلة أي مخروط إلى واحد من ثلاثة أشكال ص بسيطة: x 2 / a 2 + y 2 / b 2 = 1 ، x 2 / a 2 - y 2 / b 2 = 1 ، أو y 2 = 2px ، المقابلة للقطع الناقص ، القطع الزائد ، القطع المكافئ ، على التوالي. (القطع الناقص حيث a = b هو في الواقع دائرة.) الاستخدام الواسع لأنظمة الإحداثيات للتحليل الجبر للمنحنيات الهندسية التي نشأت مع رينيه ديكارت (1596–1650). انظر تاريخ الهندسة: الهندسة الديكارتية.
أصول يونانية
يرتبط التاريخ المبكر للأجزاء المخروطية بمشكلة "مضاعفة المكعب". وفقًا لإيراتوستينس من Cyrene (حوالي 276-190 قبل الميلاد) ، استشار أهالي ديلوس أوراكل أبولو للمساعدة في إنهاء الطاعون (حوالي 430 قبل الميلاد) وأمروا ببناء أبولو مذبحًا جديدًا يبلغ ضعف حجم المذبح القديم وبنفس الشكل المكعب. مستغربًا ، استشار ديليانز أفلاطون ، الذي قال إن "أوراكل يعني ، ليس أن الإله أراد مذبحًا مضاعفًا الحجم ، لكنه كان يرغب في تحديد المهمة ، أن يخجل اليونانيين من إهمالهم للرياضيات واحتقارهم للهندسة ". اكتشف أبقراط خيوس (c.470-410 قبل الميلاد) لأول مرة أن "مشكلة ديليان" يمكن اختزالها لإيجاد نسبيين متناسبين بين أ و 2 أ (أحجام المذابح ذات الصلة) - أي تحديد س وص بحيث: س = س: ص = ص: 2 أ. هذا يعادل حل أي معادلتين في نفس الوقت x 2 = ay و y 2 = 2ax و xy = 2a 2 ، والتي تتطابق مع مقطعين مكافئين و hyperbola ، على التوالي. في وقت لاحق ، أظهر أرخميدس (حوالي 290-211 قبل الميلاد) كيفية استخدام المقاطع المخروطية لتقسيم المجال إلى قسمين لهما نسبة معينة.
أثبتت Diocles (c.200 قبل الميلاد) هندسيًا أن الأشعة - على سبيل المثال ، من الشمس - الموازية لمحور القطع المكافئ للثورة (التي تنتجها تدوير القطع المكافئ حول محور التناظر) تلتقي عند التركيز. يقال أن أرخميدس قد استخدم هذه الخاصية لإشعال النار في سفن العدو. استشهد Anthemius of Tralles ، أحد المهندسين المعماريين لكاتدرائية آيا صوفيا في القسطنطينية (اكتمل في الإعلان 537) ، بالخصائص البؤرية للقطع الناقص كوسيلة لضمان إضاءة المذبح بواسطة ضوء الشمس طوال اليوم.