فرضية ريمان الرياضيات

فرضية ريمان ، في نظرية الأعداد ، فرضية عالم الرياضيات الألماني برنهارد ريمان بخصوص موقع حلول دالة Riemann zeta ، والتي ترتبط بنظرية العدد الأولي ولها آثار مهمة على توزيع الأعداد الأولية. أدرج ريمان الفرضية في ورقة ، "Ueber die Anzahl der Primzahlen unter einer gegebenen Grösse" ("على عدد الأعداد الأولية أقل من كمية معينة") ، المنشورة في طبعة نوفمبر 1859 من Monatsberichte der Berliner Akademie من أكاديمية برلين ").

يتم تعريف وظيفة زيتا على أنها السلسلة اللانهائية ζ (s) = 1 + 2 ^−s + 3 ^−s + 4 ^−s + ⋯ ، أو في تدوين أكثر تعقيدًا ،

، حيث يكون الجمع (Σ) للمصطلحات لـ n يمتد من 1 إلى اللانهاية من خلال الأعداد الصحيحة الموجبة و s هو عدد صحيح موجب ثابت أكبر من 1. تمت دراسة الدالة zeta لأول مرة من قبل عالم الرياضيات السويسري Leonhard Euler في القرن الثامن عشر. (لهذا السبب ، يطلق عليها أحيانًا وظيفة Euler zeta. بالنسبة إلى ζ (1) ، هذه السلسلة هي ببساطة السلسلة التوافقية ، المعروفة منذ العصور القديمة لزيادة بلا حدود - أي أن مجموعها لا نهائي.) حقق Euler شهرة فورية عندما ثبت في عام 1735 أن ζ (2) = π ² /6، مشكلة استعصى أعظم علماء الرياضيات في العصر، بما في ذلك الأسرة برنولي السويسري (جاكوب، يوهان، ودانيال). بشكل عام ، اكتشف أويلر (1739) علاقة بين قيمة وظيفة زيتا حتى الأعداد الصحيحة وأرقام برنولي ، وهي المعاملات في توسع سلسلة تايلور لـ x / (e ^x - 1). (انظر أيضًا دالة أسية.) لا يزال الأمر الأكثر إثارة للدهشة ، في عام 1737 اكتشف أويلر صيغة تتعلق بوظيفة زيتا ، والتي تنطوي على جمع تسلسل لا نهائي من المصطلحات التي تحتوي على أعداد صحيحة موجبة ، ومنتج لا نهائي يتضمن كل رقم أولي:

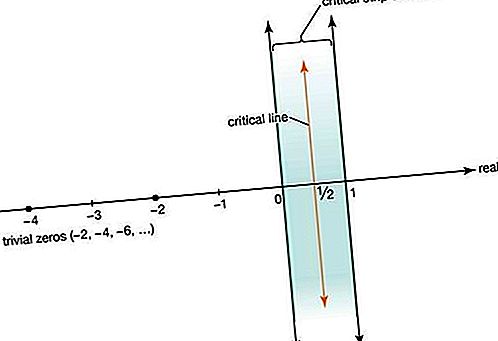
مدد ريمان دراسة دالة زيتا لتشمل الأعداد المركبة x + iy ، حيث i = الجذر التربيعي لـ √ 1 ، باستثناء الخط x = 1 في المستوى المركب. عرف ريمان أن دالة زيتا تساوي الصفر لجميع الأعداد الصحيحة السالبة حتى −2 ، −4 ، −6 ،

(ما يسمى بالأصفار التافهة) وأنه يحتوي على عدد لا نهائي من الأصفار في الشريط الحرج من الأعداد المعقدة التي تقع بدقة بين السطور x = 0 و x = 1. وهو يعلم أيضًا أن جميع الأصفار غير التافهة متماثلة فيما يتعلق بـ خط حرج س = ¹ / ₂. افترض ريمان أن جميع الأصفار غير التقليدية على الخط الحرج ، وهو التخمين الذي أصبح يعرف فيما بعد بفرضية ريمان.

في عام 1914 الرياضيات اللغة الإنجليزية ثبت غودفري هارولد هاردي أن عددا لا حصر له من حلول ζ (ق) = 0 موجود على خط حرج س = ¹ / ₂. في وقت لاحق ، أظهر علماء الرياضيات المختلفون أن نسبة كبيرة من الحلول يجب أن تكمن في الخط الحرج ، على الرغم من أن "البراهين" المتكررة على أن جميع الحلول غير البديهية عليها كانت معيبة. كما تم استخدام أجهزة الكمبيوتر لاختبار الحلول ، حيث ثبت أن أول 10 تريليون من الحلول غير التقليدية تقع على الخط الحرج.

سيكون لإثبات فرضية ريمان عواقب بعيدة المدى على نظرية الأعداد واستخدام الأعداد الأولية في التشفير.

لطالما اعتبرت فرضية ريمان أكبر مشكلة لم تحل في الرياضيات. كانت واحدة من 10 مشاكل رياضية لم يتم حلها (23 في العنوان المطبوع) تم تقديمها كتحدٍ أمام علماء الرياضيات في القرن العشرين من قبل عالم الرياضيات الألماني ديفيد هيلبرت في المؤتمر الدولي الثاني للرياضيات في باريس في 8 أغسطس 1900. في عام 2000 عالم الرياضيات الأمريكي ستيفن قام Smale بتحديث فكرة هيلبرت بقائمة من المشاكل المهمة للقرن الحادي والعشرين. كانت فرضية ريمان رقم واحد. في عام 2000 تم تصنيفها كمشكلة الألفية ، واحدة من سبع مشاكل رياضية اختارها معهد كلاي للرياضيات في كامبريدج ، ماساتشوستس ، الولايات المتحدة ، للحصول على جائزة خاصة. الحل لكل مشكلة الألفية يساوي مليون دولار. في عام 2008 ، أدرجتها وكالة مشاريع البحوث المتقدمة للدفاع الأمريكية (DARPA) كواحدة من التحديات الرياضية لـ DARPA ، 23 مشكلة رياضية كانت تلتمس مقترحات بحثية لتمويلها - "التحدي الرياضي التاسع عشر: تسوية فرضية ريمان. الكأس المقدسة لنظرية الأعداد ".